Developing a Generalized Elo Rating System for Multiplayer Games
And using it to prove that I’m a terrible poker player
I originally wrote this post on Towards Data Science before moving it here.
Elo is perhaps the best know rating system. It was originally invented to measure the relative skill of chess players, and it’s been applied to many other games since then. In recent years Elo has been popularized by FiveThirtyEight—for example, they use it for their NFL predictions. (A common misconception: Elo is not an acronym! The Elo rating system is named after its creator, Arpad Elo.)
Elo’s greatest strength is its simplicity. Each player (or team) has some rating before a game is played, and after we observe the outcome of the game we use a simple formula to calculate each player’s new Elo rating. That makes it easy to track each player’s rating over time. The ratings change as you would expect. Winning always improves a player’s rating and losing always hurts it. Beating a strong player is worth more than beating a weaker player. (More on the mathematical details later.)
An obvious shortcoming is that Elo only works for two-player games. Lots of games have more than two players—races, video games, board games, and so on—and we might want to assign ratings to players in those games. It would be nice to have a simple rating system for those games, but we’ll have to look beyond standard Elo.
I became motivated to build a multiplayer rating system after playing poker games with my friends. Poker was one of our quarantine hobbies during the COVID-19 pandemic. Once a week or so we’d hop on a video call, chip in a few dollars each, and play poker for a few hours. It was a good way to have socially distanced fun, but there was one big problem: I’m not a good poker player. That’s what I thought at the beginning, anyway, but I quickly realized I was wrong. I am a terrible poker player.
Fortunately for you, dear reader, I’m also a big nerd who likes to bring math into his hobbies. I wasn’t satisfied knowing I was a terrible poker player; I wanted to quantify precisely how terrible I was. So I developed a simple extension to the standard Elo rating system.
How Elo works
Let’s start by understanding how standard Elo works with two players. There are three steps to generating Elo ratings:
- Expected score: predict the outcome of a game.
- Actual score: observe the outcome.
- Update: increase or decrease each player’s rating based on result.
Let’s look at each step in a little more detail. To predict which player will win, we plug the each player’s current rating into a simple logistic function. Suppose we have Players A and B, with ratings \(R_A\) and \(R_B\), respectively. Then the “expected score” for Player A is
Equation 1: expected score formula for standard (two-player) Elo.
The expected score tells you how likely Player A is to win. For example, an expected score of 0.75 means Player A will beat Player B 75% of the time. A larger difference in ratings leads to a larger expected score for the higher rated player. Notice there’s a variable \(D\) in there. That’s one of the parameters that we can tune in the Elo algorithm, and it controls how the difference in ratings translates to win probabilities. It’s pretty common to set \(D = 400\).
Next we observe the results of the matchup. Let’s use the following binary representation so that we can easily compare the results to the expected scores:
Equation 2: how to encode game results in standard Elo.
Now we’re ready to update the ratings for our players. The change in a player’s rating depends on the difference in expected and observed results. The new rating for Player A is
Equation 3: updating a player's Elo rating after observing the results of a game.
It’s clear that if the observed result is greater (better) than the expected score, the rating goes up. Otherwise it goes down. The \(K\) value is another Elo parameter that roughly determines how much a player’s rating can change after a single game. It’s common to set \(K\) to some fixed value, like \(K = 32\), or some systems will vary the value of \(K\) depending on how many games a player has previously played.
Sometimes it’s helpful to walk through an example. Suppose Player A starts with a rating of 1200 and Player B starts with a rating of 1000, and suppose Player A wins the game. The equations above tell us that Player A’s expected score is \(E_A = 0.76\), actual score is \(S_A = 1\), and new rating is \(R'_A = 1207.7\). (I used \(D = 400\) and \(K = 32\) in this example.)
Extending Elo to multiplayer games
Here’s where we put our thinking caps on. Let’s see if we can modify each step of the Elo calculation to accommodate more than two players. We’ll tackle it one step at a time, following the same three steps as standard Elo.
Expected scores
Elo only knows how to compare two players at a time. Let’s reframe our multiplayer game as a combination of pairwise matchups. For example, a game with three players has three distinct matchups (A vs. B, A vs. C, and B vs. C). More generally, a game with \(N\) players has \(N(N-1)/2\) distinct pairwise matchups.
Let’s use standard Elo to compute all pairwise expected scores using the formula from the previous section. Then we’ll sum each player’s individual expected scores to get a total expected score for each player. Lastly, we’ll scale the scores so that they sum to 1 across all players (allowing us to interpret the scores as probabilities, like we do in standard Elo). In mathematical terms, our expected score for Player A looks like this:
Equation 4: Expected score calculation for multiplayer Elo. I'll leave it up to the reader to validate that the sum of all players' expected scores is 1, and that this equation converges to the standard Elo equation when \(N = 2\).
The equation looks a little unwieldy, but it’s really not so different from the standard Elo process (compare to Equation 1 above). Step one, done.
Actual scores
Next up is observing and notating the results. This was really simple for standard Elo, but it’s going to be a bit more involved here. Similar to standard Elo, we want to encode the results with a score like this:
Equation 5: General form for how we'll encode the results in multiplayer Elo.
But what exactly should be the values of \(s_1, s_2, \dots, s_N\)? With two players it was trivial—the winner gets a score of 1 and the loser gets a score of 0—but there are more possibilities with more players. Should \(s_1 = 1\), or should \(s_1 + \dots + s_N = 1\)? Should the values increase linearly from one place to the next, or should they have some other relationship? I came up with a few conditions the scores should satisfy:
- The scores must be monotonically decreasing. That is, 1st place has a higher score than 2nd, which has a higher score than 3rd, and so on.
- Last place must have a score of 0. A last-place finish should never improve a player’s rating.
- The scores must sum to 1 across all players. This way they are on the same scale as the expected scores that we defined above.
Those rules seem sensible, but there’s still more than one way to assign scores that satisfy them for \(N \ge 3\) players—in fact, there are infinitely many ways! But that flexibility is actually a good thing for our rating system. Let’s call any function that satisfies our three rules a score function. Consider the following two score functions, which we’ll call the “linear” and “exponential” score functions:
Equation 6: linear (top) and exponential (bottom) score functions. Note that the exponential score function converges to the linear score function as \(\alpha \to 1\), and both yield binary scores when \(N = 2\) (proof left to reader).
In both equations, \(N\) is the number of players and \(p_A\) is the place that Player A finishes in (1 for 1st, 2 for 2nd, …, \(N\) for last). The exponential score function has an additional parameter \(\alpha\), which we can give any value greater than 1 (I’ll also refer to it as the “base” of the exponential function). But let’s not get too hung up on the equations—it’s much clearer graphically:
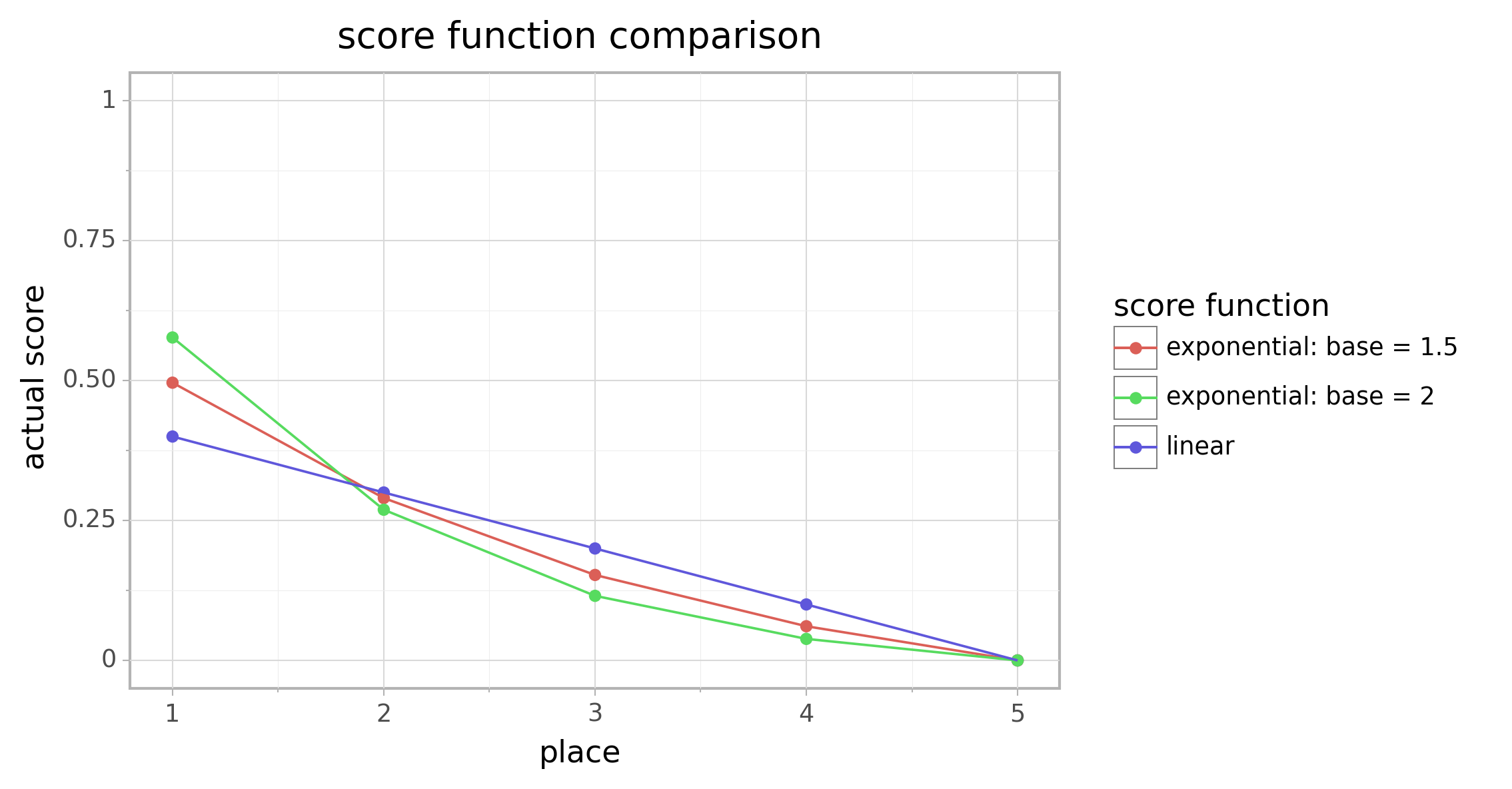
Figure 1: comparison of three different score functions for \(N = 5\) players.
There’s a clear difference in how the scoring functions share rewards between different players. The linear score function doesn’t care whether you finish near the top or the bottom—improving from 5th place to 4th is just as valuable as improving from 2nd to 1st. The exponential score function, on the other hand, gives more of the rewards to the players who finish at the top—improving from 2nd to 1st is worth a lot, while 4th is only rewarded a small amount more than 5th.
So which score function should we choose? It depends on our use case. I’m building this rating system with poker in mind, so let’s start there and see where it leads us. Imagine you’re in a poker tournament where 10 players enter and the top 3 will win money. Suppose you start off with some bad luck and find yourself running low on chips early in the game. I’m oversimplifying, but you have two basic options:
- Play passively. Try to avoid being the first player to run out of chips. You probably won’t finish in last, but you have almost no chance of winning. You’ll likely bleed chips slowly and finish near the middle or bottom.
- Be aggressive and make some high-risk, high-reward plays. If it works you’re right back in contention with a chance to win. But there’s also good chance the risk doesn’t pay off and you finish in last place.
Most poker players would agree that Strategy 2 is better. Why? Because 4th place through last place all have the same real-life reward: $0. Strategy 1 might save you the embarrassment of finishing in last, but you have no chance of winning money. Strategy 2 gives you some chance, however small, of earning a payout, so it’s a better strategy. In probabilistic terms, the expected value of your earnings is higher with Strategy 2. Sometimes in poker it’s best to think like Ricky Bobby: if you ain’t first, you’re last.
What does this have to do with score functions? We should pick the score function that most closely reflects the optimal strategy of our game. If we pick the linear score function for a poker game, our rating system will reward players who pick the suboptimal Strategy 1—by avoiding last place, they pick up a substantial number of Elo rating points. Instead we should use an exponential score function, which places more emphasis on finishing near the top. Again, that’s completely dependent on the use case. For a different type of game—maybe a racing event—we might choose to use the linear score function instead.
Updating ratings
Finally we’re ready to update each player’s Elo rating after a game. This step is almost identical to the standard two-player Elo version:
Equation 7: rating update rule for multiplayer Elo. Almost identical to standard Elo!
The only adjustment we made is that we scale by the number of players in the matchup. That way the player who wins is sufficiently rewarded for beating \(N-1\) other players rather than just one.
And that’s it! We have a generalized version of Elo that works for games with more than two players! My favorite property of this rating system is that it converges to standard Elo when you only have two players—plug in \(N = 2\) to the formulas and you can see why. That’s why we can think of this as a generalized version of Elo rather than a brand new rating system.
Handling ties
Some games allow ties (including chess, which Elo ratings were invented for). In standard two-player Elo, when players tie each gets an actual score of 0.5. In multiplayer Elo we calculate the actual scoring curve as normal, then average the corresponding values for all players who tied. This way the actual scores still sum to 1 and the rest of the calculations can continue as normal.
Python implementation
Now we have a methodology. Great. How can we actually use it?
I built a Python package! You can install it from my multielo repository on GitHub. The README and demo notebook should have all of the information you need to get started.
The package primarily implements the math from the previous section, plus some classes and functions for tracking Elo ratings over time for many players. It also includes a few things that I won’t discuss in this article, such as simulating win probabilities for players in a multiplayer game. If you have questions about the package, let me know here or on GitHub!
Show me some results already!
All right, it’s finally time to throw some real data at this thing. Behold my sad poker journey:

The Elo history of all players in my poker group. Ouch.
As things currently stand, I have a stranglehold on last place which gets stronger with each passing game. Miraculously, I won the first game (notice the small upward blip at the far left) but that must have been beginner’s luck. It’s been all downhill from there.
I created that chart by calculating each player’s new Elo rating at the end of every game. Each player starts at 1000 (an arbitrary value) and then moves up or down depending on their results. The change in a player’s rating after each game depends on where they finished and which other players were involved.
[Poker fans: one thing to note is that we played tournament style games, so it’s always clear who finished first, second, third, and so on. This type of rating system couldn’t be applied as easily if we were playing cash games instead, where there aren’t necessarily clear winners and losers at the end of the game.]
Interactive web app
If you want to see the ratings in more detail, check out the web app that I built here sorry, you can’t!
Blame Heroku for getting rid of their free tier.
But you can look at this GIF I created when my web app was still up and running:
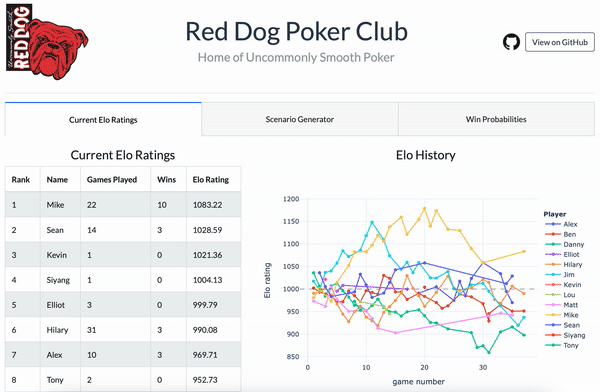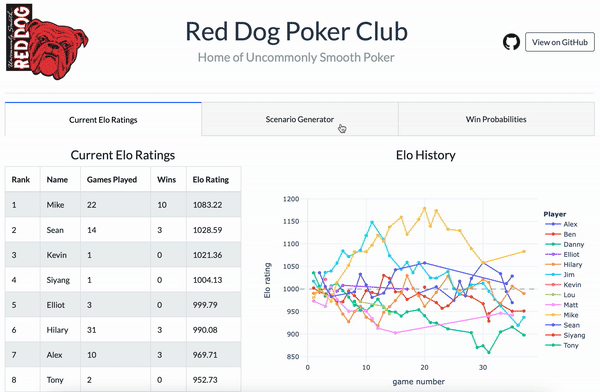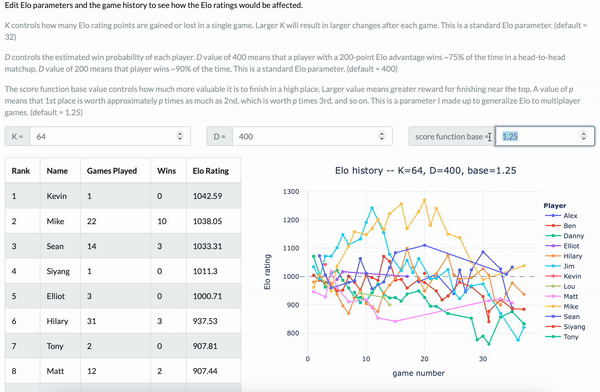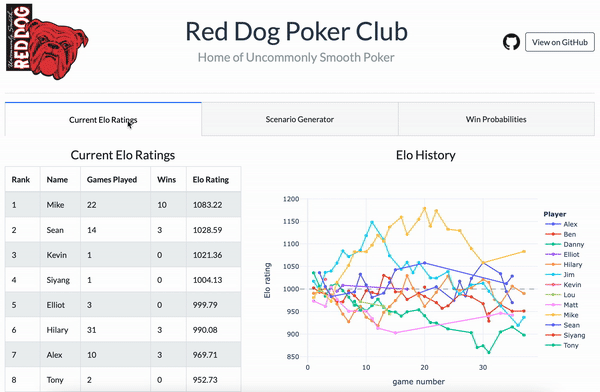
Demo of the web app I created for my poker group. (Yes, it’s named after an obscure Wisconsin beer.)
In the app you’ll find a full history of our poker games, plus some tools for editing the game history and the Elo parameters to see how it would affect the ratings.
I built the app using Dash, a popular framework for creating dashboards and web apps using only Python. The app reads data from a Google Sheets spreadsheet and uses my multielo package to calculate Elo ratings. The app is hosted on the cloud platform Heroku, which lets you host small web apps for free (or rather, they did until November 2022).
The source code for the web app is also available on GitHub. This was the first Dash app that I built and it was pretty easy to get started.
Tags: data analysis rankings web apps python poker